Source: yuliandini201831070.blogspot.com
KEMONOTONAN DAN KECEKUNGAN KURVA Pada bagian ini penggunaan turunan akan di titik beratkan untuk mengetahui sifat-sifat yang dimiliki suatu kurva antara lain kemonotonan kecekungan nilai ekstrim titik belok dan asymtot.
Source: encrypted-tbn0.gstatic.com
Dari uraian penerapan pada fungsi kuadrat tersebut dapat dilihat bahwa luas daerah yang dibatasi oleh dua buah kurva cekung baik keduanya cekung ke atas maupun.
Source: id.natapa.org
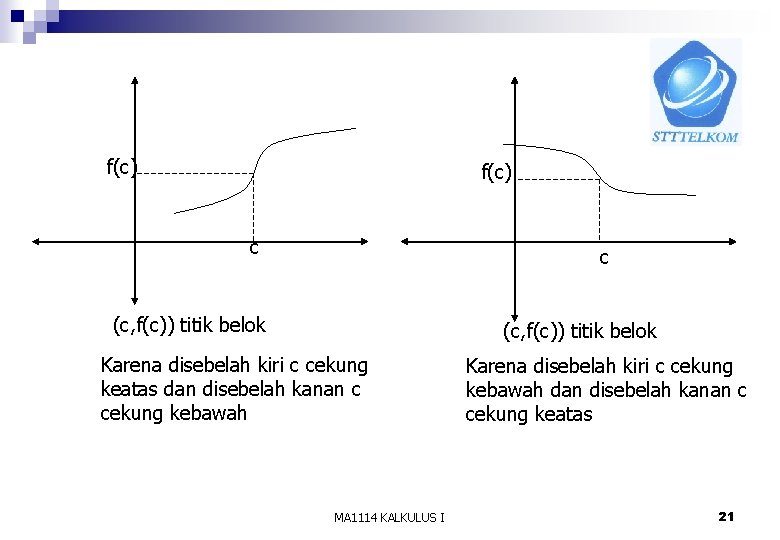
Titik a f a b f b dan c f c disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya.
Source: www.masdayat.net
Fungsi dikatakan cekung ke atas pada interval bila naik pada interval sedang dikatakan cekung ke bawah bila turun pada interval.
Source: id.quora.com
X 2 maka f2 122 12 12 0 cekung ke atas atau 1 Sehingga interval cekung bawah adalah x 1 dan interval cekung atas adalah x.
Source: www.andrepradnya.com
Ii Jika f x 0 untuk semua x dalam ii Jika f x 0 untuk semua x dalam ab maka f cekung ke bawah pada ab.
Source: www.slideshare.net
Uji Kecekungan Fungsi Interval kecekungan suatu fungsi dapat ditentukan dari turunan kedua fungsi tersebut.
Source: www.youtube.com
Ii Jika f x 0 untuk semua x dalam ii Jika f x 0 untuk semua x dalam ab maka f cekung ke bawah pada ab.
Source: www.slideshare.net
Pembahasan Dengan menurunkan fungsi yang diberikan dua kali dihasilkan Berdasarkan turunan kedua f tersebut kita dapat melihat bahwa tidak ada nilai x yang menyebabkan f x 0 tetapi pada x 2 fungsi f tidak kontinu.
Source: edumatik.net
Pembahasan Dengan menurunkan fungsi yang diberikan dua kali dihasilkan Berdasarkan turunan kedua f tersebut kita dapat melihat bahwa tidak ada nilai x yang menyebabkan f x 0 tetapi pada x 2 fungsi f tidak kontinu.
Source: slideplayer.info
Titik a f a b f b dan c f c disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya.
Source: www.masdayat.net
Ilustrasi mudahnya untuk mengingat kecekungan fungsi yaitu dengan membayangkan mangkuk sebagai cekung ke atas dan mangkuk terbalik sebagai cekung ke bawah.
Source: dosen.perbanas.id
Fungsi f cekung ke atas jika fx 0 24x - 16 0 24x 16 x 23 Fungsi f cekung ke bawah jika fx 0 24x - 16 0 24x 16 x 23 Titik belok fungsi f diperoleh jika fx 0 24x - 16 0 24x 16 x 23 f234 1727 Titik beloknya 234 1727.
Source: slideplayer.info
Titik a f a b f b dan c f c disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya.
Source: www.andrepradnya.com
Pembahasan Dengan menurunkan fungsi yang diberikan dua kali dihasilkan Berdasarkan turunan kedua f tersebut kita dapat melihat bahwa tidak ada nilai x yang menyebabkan f x 0 tetapi pada x 2 fungsi f tidak kontinu.
Source: brainly.co.id
Uji Kecekungan Fungsi Interval kecekungan suatu fungsi dapat ditentukan dari turunan kedua fungsi tersebut.
Source: brainly.co.id
Ilustrasi mudahnya untuk mengingat kecekungan fungsi yaitu dengan membayangkan mangkuk sebagai cekung ke atas dan mangkuk terbalik sebagai cekung ke bawah.
Source: brainly.co.id
Untuk menerapkan Teorema Uji Kecekungan tentukan lokasi nilai-nilai x sedemikian sehingga f x 0 atau f tidak ada.
Source: amatiory.blogspot.com
Yaitu fungsi di mana garis yang menghubungkan dua titik dalam grafik tidak pernah berada di bawah grafik.
Source: www.masdayat.net
Uji Kecekungan Fungsi Interval kecekungan suatu fungsi dapat ditentukan dari turunan kedua fungsi tersebut.
Source: www.youtube.com
Pembahasan Dengan menurunkan fungsi yang diberikan dua kali dihasilkan Berdasarkan turunan kedua f tersebut kita dapat melihat bahwa tidak ada nilai x yang menyebabkan f x 0 tetapi pada x 2 fungsi f tidak kontinu.
Source: docplayer.info
Selain ituBentuk cermin cekung berupa lengkungan yang teratur dan permukaannya yang melengkung ke dalam.
Source: studylibid.com
Fungsi dikatakan cekung ke atas pada interval bila naik pada interval sedang dikatakan cekung ke bawah bila turun pada interval.
Source: edscyclopedia.com
KEMONOTONAN DAN KECEKUNGAN KURVA Pada bagian ini penggunaan turunan akan di titik beratkan untuk mengetahui sifat-sifat yang dimiliki suatu kurva antara lain kemonotonan kecekungan nilai ekstrim titik belok dan asymtot.
Source: www.andrepradnya.com
Suatu fungsi dikatakan cekung ke atas jika turunan pertama dari fungsi tersebut naik cekung ke bawah jika turunan pertama dari fungsi tersebut turun pada suatu interval terbuka.